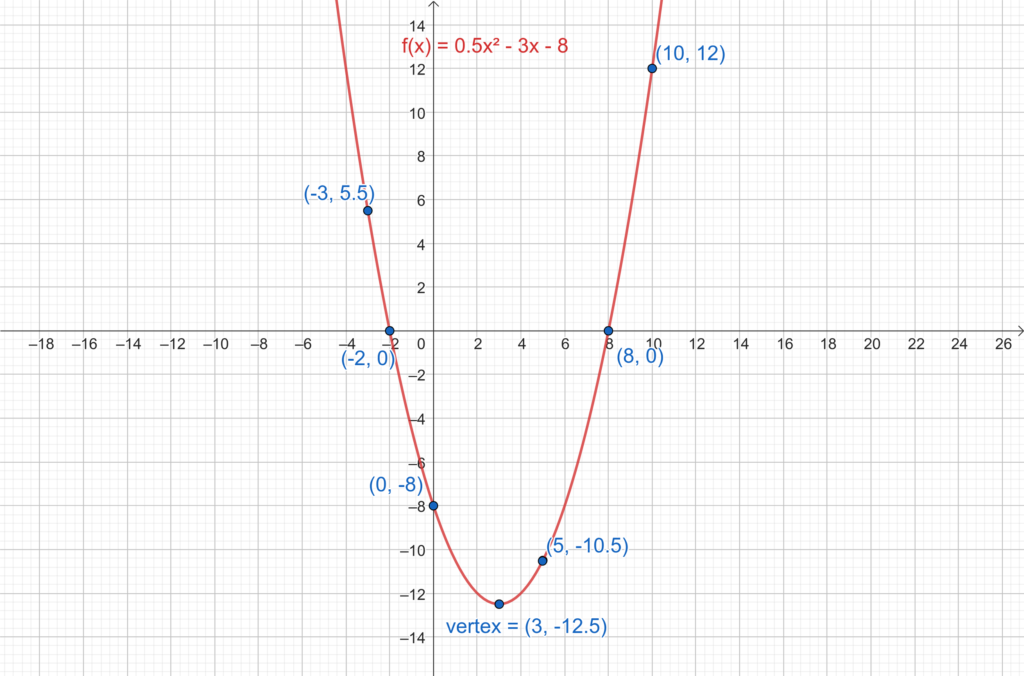
Have you ever wondered how to visually represent a function? Graphing a function is more than just plotting points; it’s about understanding the relationship between variables. Whether you’re tackling algebra or diving into calculus, knowing how to graph functions can unlock deeper insights into mathematical concepts.
Understanding Functions
Functions form the backbone of mathematics, providing a structured way to express relationships between variables. A function connects an input with exactly one output, making it essential for graphing and analysis.
Definition of a Function
A function is a relationship that assigns each input exactly one output. For example, in the function ( f(x) = 2x + 3 ), every value of ( x ) has a unique corresponding ( y ). In this case, if you plug in ( x = 1 ), you get ( f(1) = 5 ). This clarity allows for precise calculations and graphing.
Types of Functions
Functions can be categorized into several types based on their characteristics:
- Linear Functions: These functions create straight lines when graphed. An example is ( f(x) = mx + b ).
- Quadratic Functions: These produce parabolas on graphs, like ( f(x) = ax^2 + bx + c ).
- Exponential Functions: They grow rapidly and are represented as ( f(x) = ab^x ).
Understanding these types helps you identify how different functions behave, aiding in accurate graphing and interpretation.
Preparing to Graph a Function
Preparing to graph a function involves gathering the right tools and selecting an appropriate function type. This foundation ensures accuracy and clarity in your graphical representation.
Tools You Will Need
You’ll need specific tools to effectively graph functions:
- Graph Paper: Provides a structured background, making it easier to plot points accurately.
- Ruler: Ensures straight lines for linear functions, enhancing visual clarity.
- Pencil and Eraser: Allows for corrections as you refine your graph.
- Calculator: Helps compute values quickly, especially for complex functions.
- Software or Apps: Programs like Desmos or GeoGebra can simplify graphing by providing interactive features.
Choosing the Right Function
Choosing the right function is crucial for effective graphing. Start with common types such as:
- Linear Functions (e.g., f(x) = mx + b): Represent constant rates of change; easy to visualize with straight lines.
- Quadratic Functions (e.g., f(x) = ax² + bx + c): Create parabolas; useful for modeling projectile motions.
- Exponential Functions (e.g., f(x) = ab^x): Show rapid growth or decay; ideal for population studies.
Consider what you want to illustrate. Are you analyzing trends over time? Then a linear function might be best. Exploring growth patterns? An exponential function works well. Each choice impacts how well your data conveys its message.
Steps to Graph a Function
Graphing a function involves several systematic steps. Each step contributes to accurately representing the relationship between variables.
Identifying Key Features
Identifying key features of the function simplifies the graphing process. Look for:
- Y-intercept: This is where the graph crosses the y-axis. For f(x) = 2x + 3, it’s (0, 3).
- X-intercepts: These points occur where f(x) = 0. Solve for x; here, x = -1.5.
- Slope: The slope indicates how steep the line is; for this linear function, it’s 2.
Understanding these features provides insight into how to plot the function effectively.
Plotting Points
Plotting points requires calculating multiple values of x and their corresponding f(x). Consider using:
- Choose x-values: Select at least five values around your intercepts, such as -2, -1, 0, 1, and 2.
- Compute f(x): Calculate each corresponding output:
- For x = -2: f(-2) = -1
- For x = -1: f(-1) = 1
- For x = 0: f(0) = 3
- For x = 1: f(1) = 5
- For x = 2: f(2) = 7
- Mark these points on your graph paper or software.
This method ensures you have enough information to represent the function accurately.
Drawing the Graph
Drawing the graph involves connecting plotted points with a straight line or curve based on function type.
- Use straight lines for linear functions like f(x) = 2x + 3.
- Draw smooth curves for quadratic functions like g(x) = x².
Start by connecting your plotted points seamlessly while paying attention to slopes and curvature. Make sure your axes are labeled clearly with appropriate scales to enhance readability and accuracy in interpretation.
Common Mistakes to Avoid
Graphing functions can become tricky, and avoiding common mistakes enhances accuracy. Here are key pitfalls to steer clear of.
Overlooking Domain and Range
You might overlook the domain and range when graphing a function. The domain consists of all possible input values (x-values), while the range includes all potential output values (y-values). For instance, in the function f(x) = √x, the domain is x ≥ 0 because negative inputs aren’t valid. If you ignore these limitations, your graph could misrepresent the function’s behavior.
Misinterpreting Function Behavior
Misunderstanding how a function behaves often leads to inaccurate graphs. Different functions exhibit unique characteristics; for example, linear functions show constant rates of change while quadratic functions curve upwards or downwards. When grappling with f(x) = x², remember it opens upward and has a vertex at (0,0). Failing to recognize these traits may cause confusion about what the graph conveys—leading you astray in your analysis.