Have you ever wondered how to graph a circle with precision? Understanding the fundamentals can transform your approach to geometry and enhance your problem-solving skills. Graphing a circle isn’t just about drawing; it’s about visualizing mathematical concepts that have real-world applications.
Understanding Circles
Understanding circles involves grasping their definition and key characteristics. A strong foundation in these concepts aids in accurately graphing circles.
Definition of a Circle
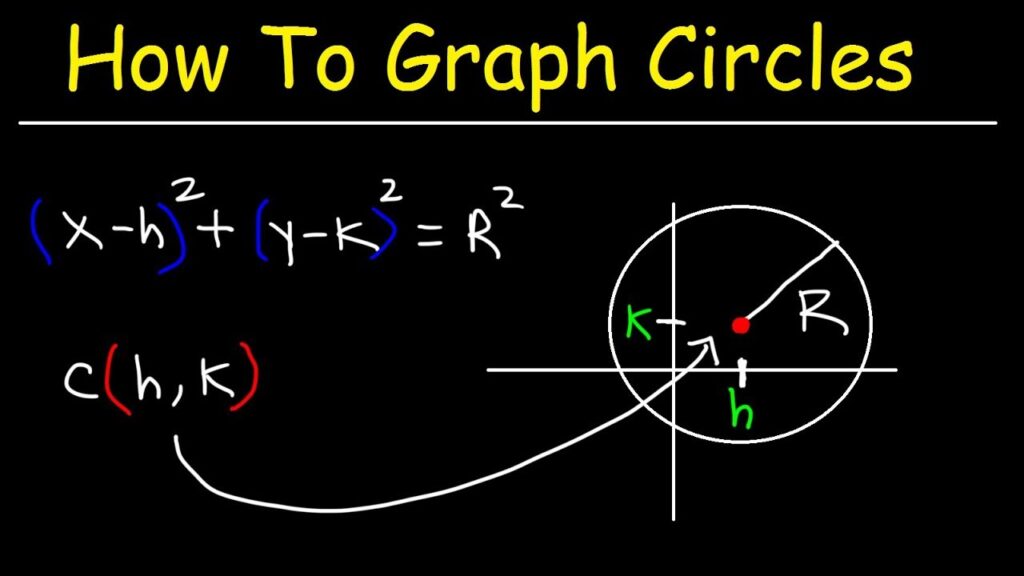
A circle is defined as the set of all points in a plane that are equidistant from a fixed point called the center. This distance is known as the radius. For example, if the center of a circle is at (0, 0) and the radius is 5, every point on the circle maintains that same distance from (0, 0).
Key Characteristics of Circles
Several key characteristics define circles:
- Center: The fixed point around which all points on the circle revolve.
- Radius: The constant distance from the center to any point on the circumference.
- Diameter: The longest distance across the circle, passing through the center; it equals twice the radius.
- Circumference: The total distance around the circle, calculated using (C = 2pi r).
- Area: The space enclosed by a circle, found with (A = pi r^2).
These elements work together to form a complete understanding of what makes up a circle and how you can effectively graph one.
Tools Needed for Graphing a Circle
Graphing a circle requires specific tools to ensure accuracy and clarity. Using the right tools simplifies the process and enhances your understanding of geometric principles.
Graphing Paper
Graphing paper provides a structured layout for plotting points effectively. Each square represents a unit, making it easier to maintain precision while graphing your circle. To utilize graphing paper:
- Identify the center of your circle.
- Mark the radius along both axes.
- Connect these points smoothly to form a perfect circle.
By using this method, you create an accurate representation of your circle without guesswork.
Graphing Software
Graphing software offers advanced features for creating circles digitally. Programs like GeoGebra or Desmos allow you to input equations directly, instantly visualizing circles based on their mathematical properties. With graphing software:
- Enter the equation of your circle in standard form (e.g., ((x – h)^2 + (y – k)^2 = r^2)).
- Adjust parameters like center ((h,k)) and radius (r) easily.
- Explore dynamic changes by modifying values in real-time.
These tools enhance learning by providing immediate feedback and visualization options that traditional methods may lack.
Steps for Graphing a Circle
Graphing a circle involves several key steps that require precision and attention to detail. Follow these steps to create an accurate representation of a circle on your graph.
Finding the Center
Identify the center coordinates of the circle. The center is usually given in the form (h, k), where h is the x-coordinate and k is the y-coordinate. For example, if you have a circle centered at (3, 2), locate this point on your graph first. Mark this point clearly; it serves as the anchor for your circle.
Determining the Radius
Determine the radius length from its equation or specification. The radius represents the distance from the center to any point on the circumference. If you’re working with a standard equation like (x – h)² + (y – k)² = r², r indicates radius length directly. For instance, if r equals 5, you’ll measure out 5 units in all directions from your center point.
Plotting Points on the Circle
Begin plotting points around your center using calculated distances based on radius. Start by moving directly up and down along vertical and horizontal lines from your center: place points at (h, k + r) and (h, k – r). Then add points horizontally at (h + r, k) and (h – r, k). For additional accuracy, use trigonometric functions or equal angular spacing around 360 degrees to find more precise locations for points on your circumference.
By following these steps systematically, you’ll effectively graph a perfect circle that accurately reflects its mathematical properties.
Common Mistakes to Avoid
When graphing a circle, several common mistakes can hinder accuracy. Recognizing these errors helps ensure a precise representation of the circle.
Misidentifying the Center
Misidentifying the center is a frequent error. The center coordinates, typically expressed as (h, k), serve as the pivotal point for your graph. If you place this point incorrectly on your graph paper or digital platform, it skews the entire circle’s shape and position. Always double-check that you’ve correctly identified and plotted these coordinates before proceeding.
Incorrect Radius Measurement
Incorrect radius measurement leads to distorted circles. The radius represents the distance from the center to any point on the circumference. Make sure you’re measuring accurately from (h, k) to points you plot around it. A common mistake is confusing diameter with radius; remember, the diameter is twice as long as the radius! Using tools like a compass can help maintain accurate measurements throughout your graphing process.