Have you ever wondered how to find the height of a triangle? Understanding this concept is essential for anyone diving into geometry. The height, or altitude, plays a crucial role in calculating the area and can help you solve various real-world problems.
Understanding Triangle Height
The height of a triangle, also known as the altitude, plays a crucial role in geometry. Height measures the perpendicular distance from a vertex to the opposite side. This measurement is essential for calculating the area of a triangle.
To find the height, you can use different methods depending on the type of triangle. For instance:
- In a right triangle, simply use one leg as the base and measure to the opposite vertex.
- For an equilateral triangle, apply the formula ( h = frac{sqrt{3}}{2} times b ), where ( b ) is the length of a side.
- In scalene triangles, draw a perpendicular line from one vertex to its opposite base and measure that line’s length.
You might wonder how these principles apply practically. Here are some examples:
- Construction projects often require knowing heights for accurate material calculations.
- Land surveying uses triangle heights to determine land elevation changes.
- Art and design may need precise measurements for triangular shapes in structures or layouts.
Importance of Finding Triangle Height
Finding the height of a triangle is crucial for various reasons. The height, also known as the altitude, plays a significant role in calculations and real-world applications.
Applications in Geometry
In geometry, calculating the area of a triangle relies on its height. You can use the formula:
[
text{Area} = frac{1}{2} times text{base} times text{height}
]
Without knowing the height, determining accurate area values becomes impossible. Additionally, understanding heights helps in classifying triangles based on their properties. For instance:
- Right Triangles: The height corresponds to one leg.
- Equilateral Triangles: Use ( h = frac{sqrt{3}}{2} b ).
- Scalene Triangles: Draw a perpendicular from one vertex to find it.
Practical Uses in Real Life
The concept of triangle height finds numerous practical applications beyond classroom settings. In construction projects, you calculate material quantities by determining areas that involve triangular shapes. Similarly, land surveying benefits from measuring heights to assess elevation changes effectively.
Also, artists need precise measurements when designing triangular elements in their work. In fields like architecture and engineering, these principles ensure designs meet safety standards while maximizing aesthetic appeal.
Understanding how to find triangle heights enhances your ability to solve complex problems efficiently across multiple disciplines.
Methods to Find the Height of a Triangle
Finding the height of a triangle can be accomplished through various methods, depending on the available information. Here are some effective techniques for determining triangle height.
Using the Base and Area
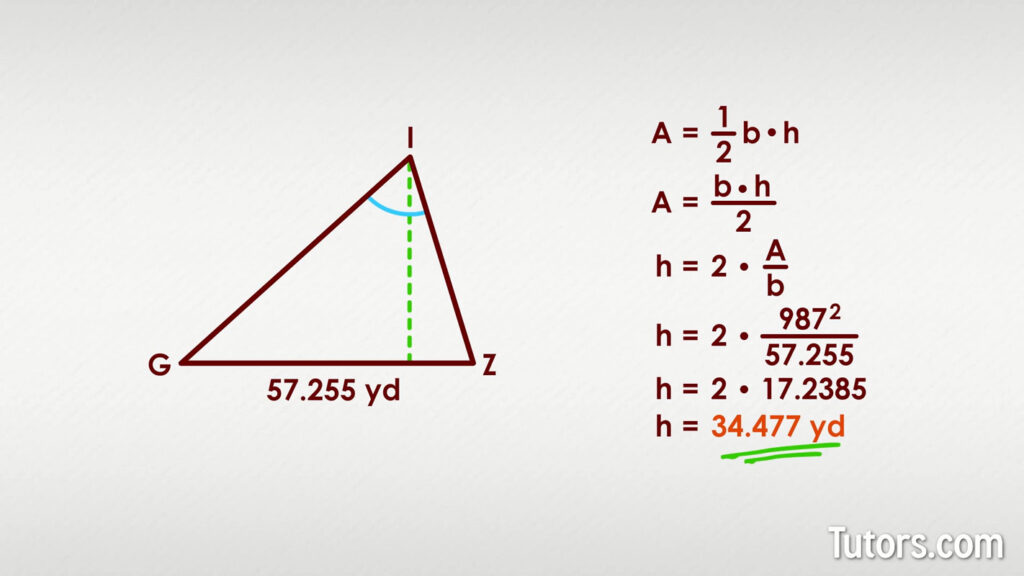
To find the height using base and area, you need two key values: the base length and the area of the triangle. The formula is:
[
text{Height} = frac{2 times text{Area}}{text{Base}}
]
For example, if you have a triangle with an area of 30 square units and a base length of 10 units, plug in these values:
[
text{Height} = frac{2 times 30}{10} = 6
]
The resulting height is 6 units.
Using the Pythagorean Theorem
In right triangles, applying the Pythagorean theorem helps determine heights easily. Given one leg as the base (( b )) and another leg as part of your right triangle’s altitude (( h )), use:
[
h^2 + b^2 = c^2
]
where ( c ) represents the hypotenuse. For instance, if ( b = 4 ) units and ( c = 5 ) units:
- Compute ( h^2 + 4^2 = 5^2 ).
- That simplifies to ( h^2 + 16 = 25 ).
- Thus, ( h^2 = 9; h = 3 ).
Here, you’ve found that the height measures 3 units.
Using Trigonometric Ratios
Trigonometric ratios provide another method for calculating heights in triangles when angles are known. You can use sine for this purpose:
[
h = b times sin(theta)
]
where ( b ) is any side adjacent to angle ( θ ). If you know that angle ( θ = 30^circ) and side length (base) is 10 units, calculate it like this:
- Identify that sin(30°) equals 0.5.
Thus,
(
h = 10 × sin(30°)
= 10 × 0.5
= 5
)
So here too, you’ve determined that the height equals 5 units.
Each method effectively finds triangle heights based on different parameters or characteristics present within your problem context.
Common Mistakes to Avoid
When finding the height of a triangle, several common mistakes can lead to incorrect calculations.
First, many forget that the height must be perpendicular to the base. If you measure at an angle, your result won’t reflect the true height. Ensure you’re drawing a straight line from the vertex straight down to the base.
Second, using incorrect formulas also causes confusion. For right triangles, remember ( h = text{leg} ) when considering one leg as the base. For equilateral triangles, use ( h = frac{sqrt{3}}{2} times b ).
Third, students often neglect units during calculations. Mixing different measurement units can produce inaccurate results. Always convert measurements to a consistent unit before performing calculations.
Finally, relying solely on visual estimation leads to errors in height assessment. Instead of guessing heights based on appearance, utilize precise methods like area calculation or trigonometric ratios for accuracy.
By avoiding these pitfalls, you enhance your ability to find triangle heights accurately and confidently.