Understanding the domain and range of a function is crucial for mastering mathematics. Have you ever wondered how to determine the values that a function can take? This knowledge not only enhances your problem-solving skills but also deepens your comprehension of various mathematical concepts.
Understanding Functions
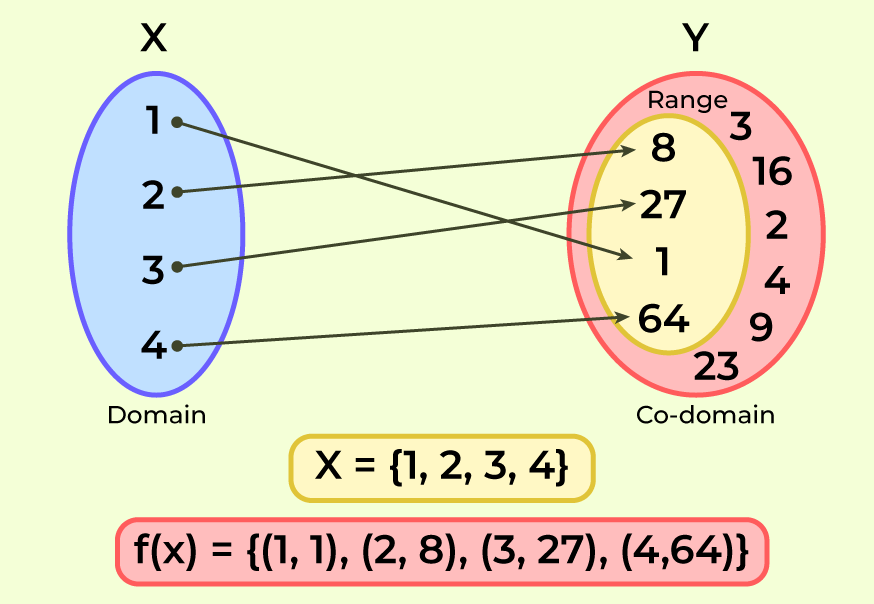
Understanding functions is crucial in mathematics. A function defines a relationship between two sets of values, where each input corresponds to exactly one output. Knowing how these relationships work enhances your mathematical skills and problem-solving abilities.
What Is a Function?
A function consists of an input set known as the domain and an output set called the range. For example, in the function f(x) = x + 2, every real number you plug into x yields a unique result by adding two. The domain includes all real numbers, while the range consists of all real numbers greater than or equal to two.
Types of Functions
Functions can be categorized based on their characteristics:
- Linear Functions: These functions create straight lines when graphed. An example is f(x) = 3x + 1, with a constant rate of change.
- Quadratic Functions: These form parabolas on graphs. For instance, f(x) = x² shows a U-shaped curve.
- Polynomial Functions: Comprising multiple terms with varying degrees, like f(x) = 2x³ – 4x + 1.
- Rational Functions: These are fractions involving polynomials; for example, f(x) = (x + 1)/(x – 1).
Identifying types helps determine their behavior and find domains and ranges efficiently.
Finding the Domain
Understanding how to find the domain of a function is crucial in mathematics. The domain represents all possible input values for which the function is defined.
Definition of Domain
The domain of a function is the complete set of possible values (inputs) that can be plugged into that function without causing any issues. For instance, in the function (f(x) = sqrt{x}), your inputs must be non-negative numbers because you can’t take the square root of negative numbers in real numbers. Therefore, the domain here is (x geq 0).
Techniques to Determine Domain
Several techniques help determine a function’s domain effectively:
- Identify Restrictions: Check for values that lead to undefined results like division by zero or negative square roots.
- Analyze Function Types: For linear functions, every real number serves as an input. In contrast, rational functions might exclude certain values due to denominators.
- Use Graphing Tools: Plotting the function can visually reveal where it exists and where it does not.
By applying these methods, you’ll gain clarity on what inputs are acceptable for various functions.
Finding the Range
Finding the range of a function includes identifying all possible output values. This process helps you understand what results a function can produce based on its inputs.
Definition of Range
The range refers to the set of all possible output values that a function can yield. In mathematical terms, if you have a function ( f(x) ), then the range is the collection of all ( f(x) ) values for every input ( x ) in its domain. For instance, consider the quadratic function ( f(x) = x^2 ). The range here consists of all non-negative numbers since squaring any real number cannot result in a negative value.
Techniques to Determine Range
Several techniques help determine the range effectively:
- Graphing: Plotting the function visually illustrates which y-values are achievable.
- Algebraic Analysis: Analyzing equations allows you to solve for y-values directly. For example, with ( y = 3x + 2 ), any real number can be achieved by adjusting x.
- Evaluating End Behavior: Understanding how functions behave as inputs approach infinity or negative infinity provides insights into potential maximum and minimum outputs.
- Using Inequalities: If your function involves inequalities, such as ( y < x + 5 ), this indicates that y is limited in its upper boundary.
By utilizing these methods, you gain clarity on what outputs are feasible for various functions and enhance your mathematical understanding significantly.
Examples of Domain and Range
Understanding the domain and range of different types of functions can enhance your grasp of mathematical concepts. Here are examples for three common function types.
Linear Functions
For a linear function like ( f(x) = 2x + 3 ), the domain includes all real numbers, as you can input any value for ( x ). The range also consists of all real numbers since every output corresponds to some input. In this case:
- Domain: All real numbers
- Range: All real numbers
Why is this important? It shows that linear functions create a straight line without restrictions.
Quadratic Functions
Consider a quadratic function such as ( f(x) = x^2 – 4 ). The domain remains all real numbers because you can plug in any ( x ) value. However, the range changes; it only includes values greater than or equal to -4, since squaring a number can’t produce negatives. Thus:
- Domain: All real numbers
- Range: ( y geq -4 )
You see how this restriction on outputs highlights key characteristics of parabolas?
Rational Functions
Take the rational function ( f(x) = frac{1}{x – 2} ). Here, the domain excludes ( x = 2), where the function becomes undefined. So, your domain looks like:
- Domain: All real numbers except ( x = 2)
The range, however, covers all real numbers except zero since no output leads back to that value:
- Range: All real numbers except zero
Isn’t it fascinating how rational functions impose specific limitations?