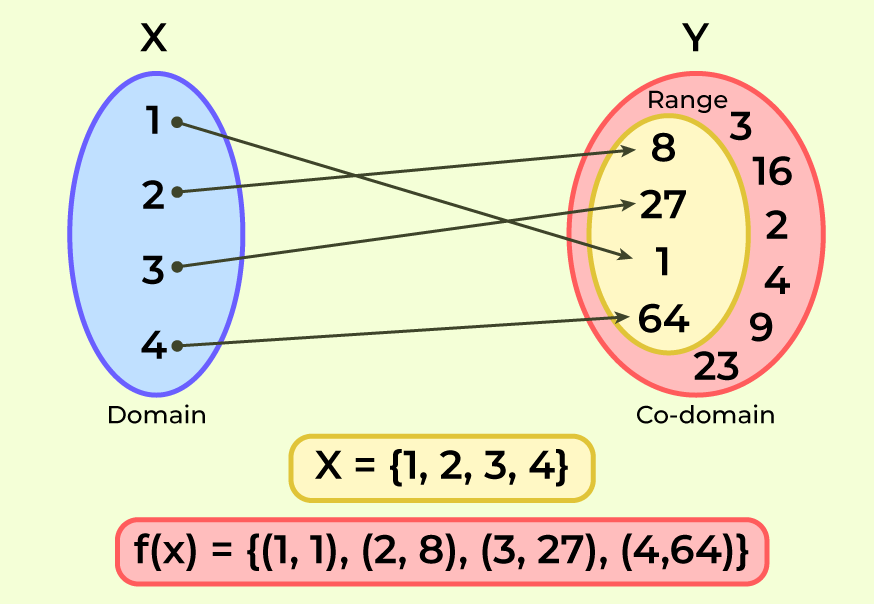
Understanding the domain and range of a function is crucial for mastering algebra and calculus. Have you ever wondered how to determine what values a function can take? Knowing the domain helps you identify all possible input values, while the range reveals all potential outputs.
Understanding Functions
Functions represent relationships between sets of inputs and outputs. Each input corresponds to exactly one output, which is crucial for determining the domain and range.
The domain includes all possible input values a function can accept. For example, consider the function ( f(x) = sqrt{x} ). Here, the domain consists of all non-negative numbers since you can’t take the square root of negative values.
The range encompasses all potential output values that result from those inputs. Using the same function ( f(x) = sqrt{x} ), the range also includes non-negative numbers because square roots yield only positive results.
You might encounter functions defined by equations or graphs. For instance, with a linear function like ( g(x) = 2x + 1 ), both the domain and range include all real numbers since they can take any value without restriction.
Additionally, when dealing with rational functions such as ( h(x) = frac{1}{x-2} ), you notice that the domain excludes specific values, particularly where division by zero occurs (in this case, ( x = 2 )). Thus, its domain is all real numbers except 2.
Understanding these concepts helps in identifying not just domains and ranges but also in solving complex problems in algebra and calculus more effectively.
Importance of Domain and Range
Understanding the domain and range of a function plays a crucial role in grasping mathematical concepts. The domain represents all possible input values, while the range covers all potential output values. Knowing these helps you analyze functions accurately, which is vital for problem-solving.
Definition of Domain
The domain consists of all valid inputs for a function. For instance, in the function ( f(x) = frac{1}{x-3} ), you cannot use ( x = 3 ) since it results in division by zero. Therefore, its domain includes all real numbers except 3. This exclusion clarifies how to work with various types of functions.
Definition of Range
The range refers to all possible outputs that a function can produce based on its domain. For example, consider the quadratic function ( g(x) = x^2 ). Its output is always non-negative because squaring any real number yields zero or more. Thus, the range is from 0 to positive infinity. Knowing this assists you in visualizing how functions behave under different conditions.
Methods to Find Domain and Range
Understanding how to find the domain and range is essential for analyzing functions. You can utilize different methods, such as graph analysis and algebraic techniques.
Analyzing Graphs
When you analyze a graph, start by identifying the x-values for which the function exists. For instance, if a graph shows a parabola that opens upward, its domain includes all real numbers. The range consists of y-values starting from the vertex point upwards.
- Look for intercepts: The x-intercepts indicate where the function crosses the x-axis.
- Check asymptotes: Vertical asymptotes often signal restrictions in domain.
- Examine endpoints: If it’s defined on an interval, note whether those endpoints are included.
Algebraic Methods
Algebraic methods provide another approach to determine domain and range effectively. You can analyze equations directly.
- Identify restrictions:
- For rational functions like ( f(x) = frac{1}{x-3} ), exclude values causing division by zero.
- Set up inequalities:
- In quadratic equations like ( g(x) = x^2 ), observe that outputs are always non-negative (range starts at 0).
- Solve for variable isolation:
- Rearranging equations helps uncover possible output values; solving ( h(x) = 0 ) can identify critical points.
By combining these methods effectively, you gain clarity on both domain and range in various types of functions without ambiguity or confusion.
Common Functions and Their Domain and Range
Understanding the domain and range of various functions helps in grasping their behavior. Here’s a look at common function types along with their respective domains and ranges.
Polynomial Functions
Polynomial functions, like ( f(x) = x^2 – 3x + 2 ), have a domain of all real numbers. This means you can input any real number into the function without restriction. The range, however, depends on the degree of the polynomial. For example, ( f(x) = x^2 ) has a range from 0 to positive infinity since it only outputs non-negative values.
Rational Functions
Rational functions feature ratios of polynomials, such as ( g(x) = frac{x+1}{x-2} ). The domain excludes any value that makes the denominator zero, which in this case is ( x = 2 ). Thus, its domain consists of all real numbers except for 2. The range varies, but generally includes all real numbers except for specific horizontal asymptotes determined by the function’s structure.
Trigonometric Functions
Trigonometric functions like ( h(x) = sin(x) ) or ( k(x) = cos(x) ) exhibit unique domains and ranges. Both have a domain of all real numbers since you can input any angle in radians. However, their range is limited to values between -1 and 1 inclusive. In contrast, tangent functions like ( m(x) = tan(x) ), exclude points where cosine equals zero (e.g., odd multiples of ( frac{pi}{2} )), leading to vertical asymptotes affecting both their domain and output values.
By examining these examples closely, you can gain insight into how different types of functions operate within algebraic frameworks.
Tips for Finding Domain and Range
Finding the domain and range of a function can be straightforward with the right techniques. Here are some effective tips to simplify the process:
- Identify Restrictions: Assess any values that might cause issues, like division by zero or square roots of negative numbers. For example, in ( f(x) = frac{1}{x-3} ), the domain excludes ( x = 3 ).
- Analyze Graphs: Look at the graph of the function to determine where it exists on the x-axis (domain) and y-axis (range). Note intercepts—these points can help clarify both aspects.
- Check Asymptotes: Vertical asymptotes indicate restrictions in domain values where functions become undefined, such as ( g(x) = frac{1}{x-2} ), which has an asymptote at ( x = 2 ).
- Use Test Points: Substitute various input values into the function to observe how outputs behave. This method often reveals potential ranges quickly.
- Consider Function Types: Recognize that different functions have specific characteristics:
- Polynomial functions generally have all real numbers as their domain.
- Rational functions may exclude certain x-values.
- Trigonometric functions exhibit periodic behavior affecting their ranges.
By applying these strategies diligently, you’ll pinpoint domains and ranges more efficiently while enhancing your understanding of functions overall.