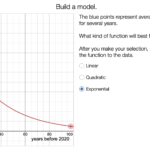
Imagine watching your investment grow at an astonishing rate or witnessing a viral trend spread like wildfire. This is the power of the exponential model, a mathematical concept that describes how certain phenomena can increase rapidly over time. Whether it’s population growth, technology adoption, or even disease spread, understanding this model can provide valuable insights into real-world scenarios.
Understanding Exponential Model
The exponential model illustrates how certain phenomena grow rapidly over time. Recognizing this pattern can enhance your understanding of various fields, from finance to biology.
Definition of Exponential Model
An exponential model describes a situation where the rate of growth is proportional to the current value. In simpler terms, as something grows, it grows faster and faster. This concept often appears in equations like (y = a cdot e^{bt}), where (a) represents the initial amount, (b) indicates the growth rate, and (t) stands for time.
Key Characteristics of Exponential Growth
Exponential growth comes with distinct features. Here are some key characteristics:
- Rapid increase: Growth accelerates over time rather than remaining constant.
- Doubling effect: The quantity doubles at regular intervals, making changes noticeable.
- Continuous process: Unlike linear growth, exponential changes occur continuously.
For example, if you invest $1,000 at an annual interest rate of 10%, after one year you’ll have $1,100. However, by the fifth year you’ll see approximately $1,610 due to compounding interest—a clear demonstration of exponential growth.
Understanding these traits helps you identify scenarios that follow this model in real life—like viral marketing campaigns or population dynamics.
Applications of Exponential Model
The exponential model finds application across various fields, demonstrating its versatility and importance. Here are some key areas where this model significantly impacts understanding and predictions.
In Population Studies
In population studies, the exponential model helps predict growth rates of organisms. For instance, in a controlled environment, bacteria can double their population every 20 minutes. This rapid increase showcases how understanding exponential growth allows scientists to estimate future populations accurately. Additionally, human populations in urban areas often display similar patterns; cities may grow exponentially based on factors like birth rates and migration.
In Finance and Economics
In finance and economics, the exponential model plays a crucial role in calculating compound interest. For example, an investment of $1,000 at an annual interest rate of 5% compounds over time. After ten years, it grows to approximately $1,628 due to the power of compounding interests driving financial growth exponentially. Economic indicators such as inflation also exhibit exponential characteristics; small percentage changes can yield significant long-term effects on purchasing power.
By leveraging the insights from these applications, you gain a clearer understanding of how the exponential model influences real-world phenomena.
Advantages of Using Exponential Model
The exponential model offers several advantages that enhance its application across various fields. Understanding these benefits can improve your insights into growth patterns and predictions.
Simplicity and Clarity
The exponential model simplifies complex phenomena. It provides a clear framework for understanding rapid growth in populations, finances, or technology adoption. With just a few parameters, you can describe how one quantity affects another over time. This clarity makes it accessible for decision-makers who need to grasp essential trends quickly without delving into complicated mathematics.
Predictive Power
The predictive power of the exponential model is significant. By analyzing past data points, you can forecast future outcomes effectively. For example:
- Population Growth: If bacteria double every 20 minutes, predictive calculations help anticipate population size after several hours.
- Investment Returns: Knowing an investment grows at a consistent rate allows you to estimate its value years down the line.
- Technology Adoption: Observing past adoption rates helps predict how quickly new technologies will reach saturation.
These capabilities enable businesses and researchers to strategize based on informed projections rather than guesswork.
Limitations of Exponential Model
The exponential model, while useful, has its limitations. Understanding these constraints is crucial for accurate application in real-world scenarios.
Assumptions and Constraints
The exponential model relies on several assumptions that may not hold true in all situations:
- Constant Growth Rate: The model assumes a constant growth rate over time. In reality, many factors can influence this rate, leading to fluctuations.
- Unlimited Resources: It presumes that resources are unlimited. However, in practical applications like population growth or resource consumption, limits often exist.
- Initial Conditions Impact Outcomes: The model’s outcomes depend heavily on initial conditions. Small variations can lead to vastly different results.
These constraints mean the exponential model might oversimplify complex systems.
Alternatives to Exponential Model
Several alternatives offer different perspectives on modeling growth:
- Logistic Growth Model: This accounts for carrying capacity and limits resource availability. It’s often used in ecology to represent populations approaching their environment’s capacity.
- Linear Models: These provide a straightforward approach but do not capture rapid growth effectively. They’re suitable for stable environments with minimal change over time.
- Power Law Models: Often applied in social sciences, they explain phenomena where large events happen less frequently compared to smaller ones.
Exploring these alternatives allows for a more nuanced understanding of growth dynamics beyond the limitations of the exponential model.