Imagine tackling complex problems with elegance and efficiency. Dynamic programming is the secret weapon of many successful programmers and developers. It’s not just a technique; it’s a mindset that transforms the way you approach challenges in coding and algorithms.
In this article, you’ll explore dynamic programming through practical examples that illustrate its power and versatility. From optimizing resource allocation to solving intricate puzzles, dynamic programming simplifies tasks that might otherwise seem daunting. Are you ready to unlock new levels of problem-solving skills?
Overview of Dynamic Programming
Dynamic programming (DP) offers efficient solutions to complex problems by breaking them down into simpler subproblems. This technique reduces computation time and avoids redundant calculations, making it essential for optimizing algorithms.
Common examples of dynamic programming include:
- Fibonacci Sequence: Instead of recalculating Fibonacci numbers repeatedly, you store previous values in an array or variable.
- Knapsack Problem: It determines the most valuable items to include in a knapsack without exceeding its weight limit. By calculating maximum value combinations incrementally, DP simplifies decision-making.
- Longest Common Subsequence (LCS): This problem finds the longest sequence present in two sequences. Using a matrix to store results helps avoid recalculating overlapping subsequences.
- Edit Distance: This algorithm calculates the minimum number of edits required to transform one string into another. DP efficiently computes these edits through a systematic approach.
These examples highlight how dynamic programming enhances efficiency and effectiveness across various applications. Your understanding of these concepts can significantly improve your coding skills and problem-solving strategies.
Core Concepts of Dynamic Programming
Dynamic programming consists of several core concepts that enhance problem-solving capabilities. Understanding these principles ensures effective implementation in various scenarios.
Memoization vs Tabulation
Memoization and tabulation are two primary techniques in dynamic programming. While both aim to optimize performance, they follow different approaches.
- Memoization stores results of expensive function calls and reuses them when the same inputs occur again.
- Tabulation, on the other hand, solves problems by filling a table iteratively, starting from the base case.
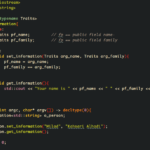
For instance, calculating Fibonacci numbers can utilize memoization to store previously computed values or tabulation to build up solutions from the bottom.
Overlapping Subproblems
Dynamic programming effectively addresses problems with overlapping subproblems. This characteristic occurs when a problem can be broken down into smaller subproblems that recur multiple times.
Consider the Fibonacci Sequence calculation: it involves computing F(n) repeatedly for various n unless optimized through dynamic programming techniques. By storing results for each Fibonacci number calculated once, you avoid redundant calculations and save time.
Optimal Substructure
Optimal substructure refers to a property where an optimal solution to a problem contains optimal solutions to its subproblems.
Take the Knapsack Problem as an example: if you determine the best way to pack items into a knapsack while maximizing value, this solution depends on finding optimal combinations of smaller subsets of items first. Thus, solving these smaller instances leads directly to solving larger ones efficiently.
Applications of Dynamic Programming
Dynamic programming finds applications in various fields, enhancing both efficiency and effectiveness. These applications range from algorithms used in computer science to solving real-world problems across different industries.
Common Algorithms
Dynamic programming underlies several well-known algorithms. Some significant examples include:
- Fibonacci Sequence: This algorithm computes Fibonacci numbers efficiently by storing values rather than recalculating them.
- Knapsack Problem: Dynamic programming optimizes resource allocation, determining the maximum value of items that can fit into a knapsack.
- Longest Common Subsequence (LCS): This algorithm identifies the longest subsequence present in two sequences, immensely useful in file comparison.
- Edit Distance: It calculates the minimum number of operations needed to transform one string into another, applicable in spell checking and DNA sequencing.
These algorithms highlight how dynamic programming simplifies complex computations while improving performance.
Real-World Use Cases
Dynamic programming extends beyond theoretical algorithms; it applies to numerous real-world scenarios:
- Supply Chain Optimization: Companies use dynamic programming for efficient inventory management and routing logistics.
- Finance: Investment strategies often rely on dynamic programming for optimal portfolio selection over time.
- Telecommunications: Network design leverages this technique to minimize costs while maximizing coverage and capacity.
- Game Development: AI characters utilize dynamic programming for decision-making processes based on multiple variables.
With these practical examples, you can see how dynamic programming plays a crucial role across various sectors.
Advantages and Disadvantages of Dynamic Programming
Dynamic programming offers several benefits. First, it significantly reduces computation time by avoiding repetitive calculations. This efficiency can save considerable processing power in larger applications. For example, algorithms like the Fibonacci Sequence demonstrate how dynamic programming minimizes redundant work.
Moreover, dynamic programming provides clear structure to complex problems. It breaks tasks into manageable subproblems, making them easier to solve individually. This approach enhances understanding and problem-solving skills.
However, there are downsides to consider. One drawback is increased memory usage due to storing intermediate results in memoization or tabulation methods. Sometimes this leads to limitations in environments with constrained resources.
Additionally, implementing dynamic programming requires a solid grasp of problem structures. If you misidentify overlapping subproblems or optimal substructure properties, the solution might become inefficient or incorrect.
In summary:
- Efficiency: Reduces computation time
- Structure: Simplifies complex problems
- Memory Usage: Can be high
- Understanding Required: Needs knowledge of specific properties
These factors highlight both the strengths and weaknesses of using dynamic programming techniques in various scenarios.