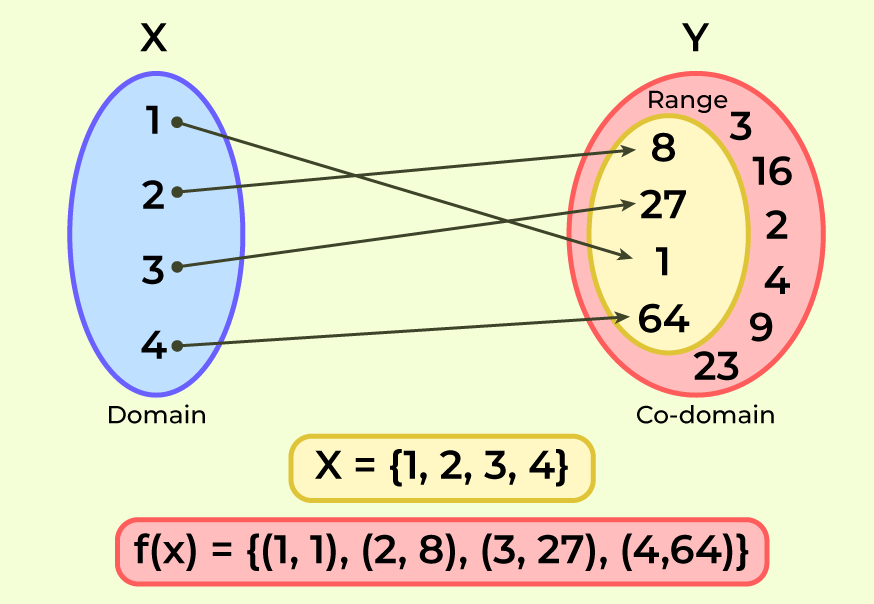
Understanding the concepts of domain and range is crucial for anyone diving into mathematics or data analysis. Have you ever wondered how to determine which values a function can take? The domain refers to all possible input values, while the range encompasses all potential outputs. Grasping these definitions can unlock deeper insights into functions and their behavior.
Understanding Domain and Range
Understanding the concepts of domain and range enhances your grasp of functions in mathematics. The domain consists of all possible input values for a function, while the range encompasses all potential output values.
Definition of Domain
The domain is crucial as it identifies which values you can plug into a function. For example, in the function ( f(x) = sqrt{x} ), the domain includes all non-negative numbers (0 and above). This restriction exists because square roots of negative numbers aren’t real. Another example is ( g(x) = frac{1}{x} ); here, the domain excludes zero since division by zero isn’t defined.
Definition of Range
The range represents all possible outputs that a function can produce based on its domain. Take ( h(x) = x^2 ); its range includes only non-negative numbers (0 and above). In contrast, consider ( k(x) = 2x + 3 ); its range covers all real numbers because linear functions have no upper or lower limits. Knowing both definitions helps predict how changes to inputs affect outputs effectively.
Importance of Domain and Range
Understanding domain and range is crucial in mathematics and data analysis. These concepts not only clarify how functions behave but also enhance your ability to predict outcomes based on input values.
Applications in Mathematics
You use domain and range extensively in various mathematical fields. For instance, when graphing functions, knowing the domain helps determine which x-values to plot. This ensures you capture the function’s behavior accurately.
- Algebra: In polynomial functions like ( f(x) = x^3 – 4x ), the domain includes all real numbers.
- Trigonometry: For ( g(x) = sin(x) ), the domain spans all real numbers, while its range varies between -1 and 1.
These examples show that understanding these aspects can significantly improve problem-solving skills.
Relevance in Real-World Scenarios
Domain and range aren’t just theoretical; they play a vital role in real-world scenarios as well. When modeling situations such as population growth or economic trends, determining valid input (domain) ensures accurate predictions.
- Finance: In calculating interest rates with ( h(t) = P(1 + r)^t ), time (t) must be non-negative.
- Physics: The trajectory of an object follows a parabolic path where its height has specific limits, defining both domain and range.
By grasping these principles, you’re better equipped to analyze data effectively across various disciplines.
How to Determine Domain and Range
Understanding how to find domain and range enhances your mathematical problem-solving skills. You can identify the input values (domain) and output values (range) of a function through various techniques.
Techniques for Finding Domain
Identifying the domain involves examining constraints on the function’s input. Here are some common methods:
- Look for restrictions: Consider functions like ( g(x) = frac{1}{x} ). The denominator cannot equal zero, so the domain excludes zero.
- Check for square roots: For ( h(x) = sqrt{x} ), you must only use non-negative numbers because square roots of negative numbers aren’t real.
- Analyze logarithmic functions: In ( f(x) = log(x) ), the input must be positive, creating another restriction on your domain.
These techniques help clarify which values can be plugged into a function.
Techniques for Finding Range
Finding the range involves determining all possible outputs from a given domain. Use these strategies:
- Graphing: Visualizing functions like ( k(x) = x^2 ) shows that outputs always remain non-negative, indicating a range of [0, ∞).
- Substituting known inputs: For linear functions such as ( m(x) = 2x + 3), any real number x results in an output across all real numbers.
- Analyzing behavior at extremes: Functions approach limits; for instance, with rational functions like ( n(x)=frac{x^2 – 1}{x}), consider what happens as x approaches infinity or negative infinity.
By applying these techniques consistently, you gain clarity on both domains and ranges in different mathematical contexts.
Common Mistakes in Identifying Domain and Range
Identifying domain and range can lead to common mistakes. Here are some frequent errors you might encounter:
- Ignoring restrictions: When determining the domain, don’t overlook values that cause undefined outcomes, like division by zero or negative square roots. For example, in ( f(x) = frac{1}{x} ), ( x ) can’t be zero.
- Assuming all real numbers: It’s easy to think every function has a domain of all real numbers. However, functions like ( g(x) = sqrt{x} ) only accept non-negative inputs.
- Misunderstanding output limits: Don’t forget that the range also has constraints based on the function’s behavior. For instance, with ( h(x) = x^2 ), the output is always non-negative.
- Overlooking piecewise functions: Piecewise functions may have different domains for each segment. Always check each part carefully before concluding the overall domain and range.
- Neglecting vertical asymptotes: Functions with vertical asymptotes will have specific exclusions in their domains, such as ( k(x) = frac{1}{x-2} ), where ( x=2 ) must be excluded.
- Failing to analyze end behavior: Sometimes you might miss how a function behaves at extremes or boundaries when finding ranges, especially with rational functions or polynomials.
Being aware of these mistakes helps improve your understanding of domain and range effectively.