Understanding central tendency is crucial for anyone diving into statistics or data analysis. Have you ever wondered how to summarize a set of numbers effectively? Central tendency provides the tools you need to do just that. It helps in identifying the “average” within your data, guiding decisions based on meaningful insights.
Overview of Central Tendency
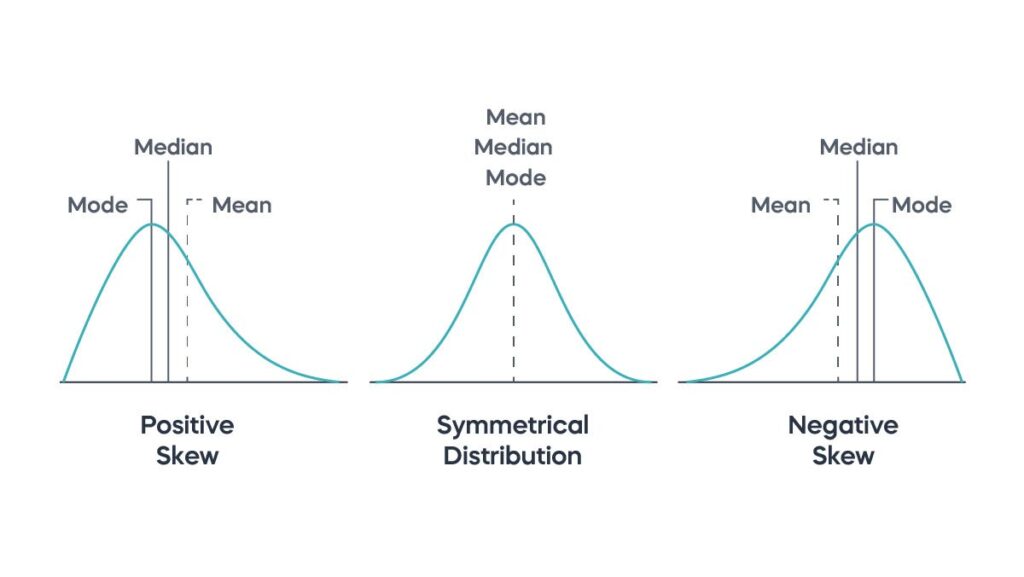
Central tendency refers to statistical measures that summarize a set of data by identifying the central point within that dataset. The three primary measures are mean, median, and mode. Each measure provides unique insights into the data’s characteristics.
- Mean: The average value, calculated by adding all numbers and dividing by the count. For instance, if you have test scores of 70, 80, and 90, the mean is (70 + 80 + 90) / 3 = 80.
- Median: The middle value in a sorted list. If your ages are 23, 25, and 30, the median is 25. If there’s an even number of values like in ages of 22, 24, and 26, then it would be (24 + 25) /2 =24.5.
- Mode: The most frequently occurring value in a dataset. In a survey with responses like red, blue, blue, green; here blue is the mode since it appears twice.
Using these measures helps you understand your data better and identify trends or patterns effectively. Data analysis becomes clearer when you know how to interpret these central tendency metrics accurately.
Measures of Central Tendency
Understanding measures of central tendency helps you summarize data effectively. The three main types—mean, median, and mode—each provide unique insights into your dataset.
Mean
The Mean represents the average value in a set of numbers. To calculate it, add all values together and divide by the total count. For example, if your data points are 10, 15, and 20:
- Add: 10 + 15 + 20 = 45
- Divide: 45 / 3 = 15
So, the mean is 15.
Median
The Median is the middle value when your data set is organized in ascending order. If there’s an even number of observations, take the average of the two middle numbers. For instance, with these values:
- Data: 7, 9, 12, 14, and 18
- Here’s how to find it:
If sorted as: 7, 9, 12, 14, and 18,
the median becomes 12 because it sits exactly in the center.
Mode
The Mode indicates which value appears most frequently within a dataset. You can have one mode (unimodal), more than one (bimodal or multimodal), or none at all if no number repeats. Consider this example:
- Data: 4, 5, 6, 5, and 7
In this case, since “5” occurs twice while others occur once or not at all,
the mode is clearly identified as 5.
By grasping these concepts—mean for averages, median for midpoints, and mode for frequency—you enhance your ability to interpret data accurately.
Importance of Central Tendency
Understanding central tendency plays a crucial role in data analysis. It provides insights that help summarize vast datasets into understandable metrics, facilitating informed decision-making.
Applications in Statistics
Central tendency measures are foundational in statistics. They assist researchers and analysts in interpreting data effectively. For instance:
- Mean: Used to determine average scores in educational assessments, giving insight into student performance.
- Median: Essential for reporting income levels, as it represents the midpoint where half earn more and half earn less.
- Mode: Useful in consumer behavior studies, identifying the most popular product among buyers.
These applications enable you to derive meaningful conclusions from raw data.
Implications in Real-World Scenarios
In real-world situations, central tendency influences various fields significantly. Consider these examples:
- Healthcare: Median patient recovery times help hospitals evaluate treatment efficacy.
- Marketing: Mode assists businesses in understanding customer preferences for product development.
- Economics: Mean income calculations inform policies aimed at economic equality.
By applying these concepts practically, you gain clearer perspectives on complex issues and trends shaping society.
Challenges with Central Tendency
Understanding central tendency presents several challenges that can impact data interpretation. These difficulties arise from the inherent limitations of each measure and potential misinterpretations in analysis.
Limitations of Each Measure
Each measure of central tendency has specific limitations that can skew results. For example:
- Mean: The mean can be heavily influenced by extreme values, known as outliers. In a dataset like 1, 2, 3, and 100, the mean is misleadingly high at 26.5.
- Median: While the median offers stability against outliers, it may not reflect overall trends in skewed distributions. In income data where most people earn low salaries but a few earn significantly more, the median might hide true disparities.
- Mode: The mode ignores all other values outside its frequency count. If you analyze survey responses where only two options receive votes while others are overlooked, it doesn’t represent broader opinions accurately.
Misinterpretations
Misinterpretations often occur when individuals overlook the context surrounding central tendency measures. For instance:
- Using only the mean to report average incomes may suggest a healthier economy than reality if there are high-income outliers.
- Relying solely on the median in populations with significant income inequality can mislead policymakers about resource allocation needs.
- Assuming that mode represents commonality without considering sample size or distribution can distort consumer behavior insights.
Recognizing these challenges helps you interpret data more critically and apply appropriate measures for clear understanding.