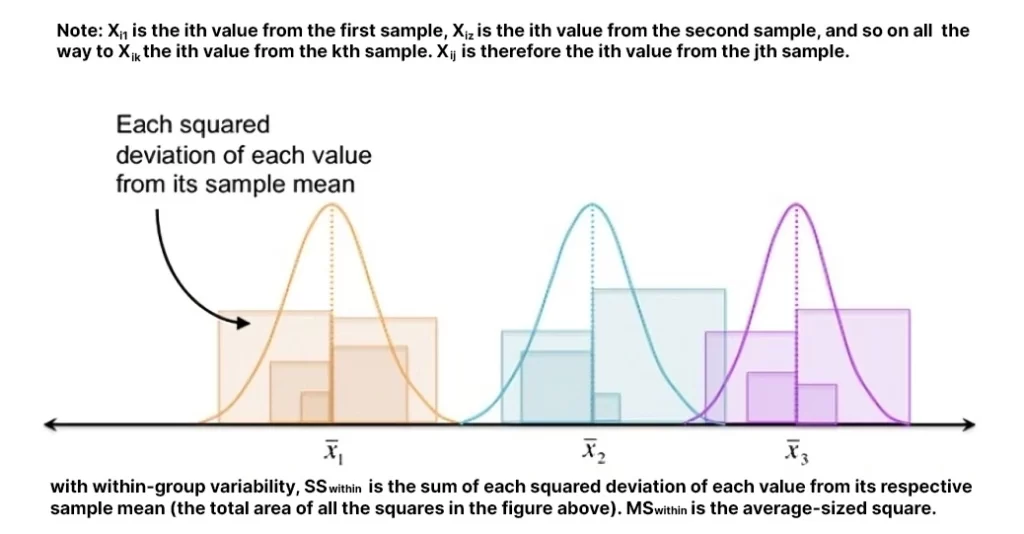
Have you ever wondered how researchers determine if different groups truly behave differently? ANOVA examples provide a powerful tool for making sense of complex data. This statistical method helps you analyze the differences among group means and is essential for anyone working with experimental data.
Understanding ANOVA
ANOVA, or Analysis of Variance, is a crucial statistical method that helps determine whether there are significant differences between the means of three or more groups. It plays an essential role in experimental research by revealing how different factors might influence outcomes.
What Is ANOVA?
ANOVA compares the variance among group means to assess if at least one group mean differs significantly from others. Essentially, it tests hypotheses about population means based on sample data. For example, in a study evaluating the effect of different diets on weight loss, researchers could use ANOVA to see if the average weight loss differs among participants following various diets.
Types of ANOVA
Different types of ANOVA cater to varying research needs. Here are some common types:
- One-Way ANOVA: This examines one independent variable with multiple levels. For instance, you might compare test scores across three teaching methods.
- Two-Way ANOVA: This assesses two independent variables simultaneously. Imagine studying how both teaching methods and student age affect test scores.
- Repeated Measures ANOVA: This analyzes data collected from the same subjects at different times. You could track patient recovery times under different treatments over several weeks.
Each type serves specific purposes and allows for comprehensive analysis tailored to your research design.
Step-by-Step ANOVA Example
Understanding how to perform ANOVA involves several key steps. Here’s a straightforward breakdown of each stage in the process.
Data Collection and Preparation
Gathering data is crucial for an effective ANOVA analysis. You typically collect samples from different groups to compare their means. For example, imagine you want to test three types of fertilizers on plant growth. Your data might look like this:
- Fertilizer A: 20 cm, 22 cm, 19 cm
- Fertilizer B: 30 cm, 28 cm, 32 cm
- Fertilizer C: 25 cm, 27 cm, 24 cm
Ensure that your samples are independent and randomly selected. This helps maintain the integrity of your results.
Performing ANOVA Analysis
ANOVA analysis involves several steps following data collection. Start by calculating the group means and overall mean. In our fertilizer example:
- Calculate means:
- Fertilizer A: (20 + 22 + 19) / 3 = 20.33
- Fertilizer B: (30 + 28 + 32) / 3 = 30
- Fertilizer C: (25 + 27 + 24) / 3 = 25.33
- Determine the total variance within groups and between groups.
- Use the F-statistic formula:
[
F = frac{text{Variance Between Groups}}{text{Variance Within Groups}}
]
- Compare your calculated F-value against a critical value from F-distribution tables at a chosen significance level (e.g., α = .05).
If your calculated F exceeds the critical value, it indicates significant differences among group means.
Interpreting ANOVA Results
Interpreting ANOVA results involves understanding key statistics that indicate whether significant differences exist among group means. Two critical components are the F-statistic and the p-value, both of which provide insights into your data analysis.
Understanding F-Statistics
F-statistics assess the ratio of variance between groups to variance within groups. A higher F-statistic suggests that group means differ significantly from each other. For example, if you observe an F-value of 5.1 in a study comparing three fertilizers’ effects on plant growth, it indicates notable differences in growth attributed to fertilizer type.
Consider these points about F-statistics:
- Higher values represent greater variation between group means.
- Lower values suggest similarities among groups.
- Critical value comparison helps determine significance.
P-Value Significance
The p-value indicates the probability that any observed difference among group means occurred by chance. A commonly used threshold is 0.05; if your p-value is below this level, you reject the null hypothesis—suggesting significant differences exist.
Here’s what to remember regarding p-values:
- P < 0.05: Significant differences detected.
- P ≥ 0.05: No significant differences found.
- Always report both the F-statistic and p-value for clarity.
In practice, if your ANOVA returns a p-value of 0.03 when testing different teaching methods’ effectiveness, it implies at least one method significantly improves student performance compared to others.
Practical Applications of ANOVA
ANOVA serves various practical applications across different fields, allowing you to analyze data effectively and make informed decisions. Here are some scenarios where ANOVA shines.
Real-World Scenarios
In education, researchers often compare teaching methods. For instance, three distinct instructional strategies might be tested on student performance. By applying One-Way ANOVA, you can determine if one method significantly enhances learning outcomes over the others.
In healthcare, scientists evaluate treatment effectiveness. Imagine comparing three different medications for lowering blood pressure. Using Two-Way ANOVA enables you to assess not only the drug’s impact but also how factors like age or gender interact with treatment results.
In marketing research, businesses gauge consumer preferences among products. You could survey customer satisfaction across multiple brands of a product. Utilizing Repeated Measures ANOVA helps track changes in satisfaction levels over time after introducing new features or promotions.
Industry-Specific Examples
Agriculture: Farmers test fertilizers’ effects on crop yields. By conducting a study involving various fertilizer types and their combinations, you can apply One-Way ANOVA to identify which combination produces the best yield statistically.
Manufacturing: Quality control teams measure defects in production processes. If you analyze defect rates across different machines using Two-Way ANOVA, it reveals whether specific machines or shifts contribute more to defects than others.
Psychology: Researchers explore therapy effectiveness by assessing patient progress under different treatment modalities. In this case, Repeated Measures ANOVA allows for tracking individual improvements over several sessions while accounting for variations between therapies.
By leveraging these examples within your field of interest, you’ll see how ANOVA becomes an invaluable tool for data analysis, helping clarify significant differences that guide decision-making processes effectively.